AI Agent Mastery: What Is an AI Agent? Definitions & Taxonomy

Issue #1 | Section 1: Foundations of AI Agents

Last week, a colleague described watching an expensive industrial robot repeatedly attempt to grasp a slightly misaligned component, failing in exactly the same way each time. Despite its impressive mechanics and programming, it lacked something crucial: the ability to perceive its environment, reason about unexpected situations, and adapt its behavior accordingly. In short, it wasn't an agent.

This distinction—between systems that merely execute procedures and those that act intelligently in uncertain environments—is at the heart of what defines an AI agent. Let's unpack this fundamental concept that underpins everything we'll explore in this newsletter series.

What Defines an AI Agent?

An AI agent is a computational system that:

1. Perceives its environment through sensors

2. Interprets this perception to form beliefs about the world

3. Decides on actions to achieve its goals

4. Acts on its environment through actuators

5. Learns from experience to improve future decisions

This perception-interpretation-decision-action loop operates continuously, enabling the agent to navigate complex, uncertain environments. Unlike simple algorithms that map inputs to outputs in a fixed way, agents maintain an internal state representing their understanding of the world and use this to inform decisions.

A critical insight often missed: an agent's effectiveness stems not from having perfect knowledge, but from handling uncertainty gracefully. The best agents don't eliminate uncertainty—they quantify and reason about it.

The Agent Taxonomy: Beyond Simple Classifications

Agents exist on multiple spectra rather than in discrete categories. Understanding these dimensions helps us design systems with appropriate capabilities:

Spectrum 1: Reactive vs. Deliberative

• Reactive agents (like a thermostat) respond immediately to environmental stimuli using simple rules

• Deliberative agents (like AlphaGo) plan multiple steps ahead, considering future consequences

Real-world insight: Most successful agents are hybrid systems, using reactive components for time-sensitive decisions and deliberative processes for complex planning. This allows them to balance responsiveness with foresight.

Spectrum 2: Individual vs. Multi-Agent

• Individual agents operate alone in their environment

• Multi-agent systems involve multiple agents interacting, cooperating, or competing

The non-obvious challenge: Designing multi-agent systems requires considering coordination mechanisms, communication protocols, and incentive structures—turning AI design into something resembling mechanism design in economics.

Spectrum 3: Degree of Autonomy

• Low autonomy: Extensive human oversight and intervention

• High autonomy: Independent operation with minimal supervision

Implementation insight: Autonomy should be graduated rather than binary. The most effective systems expand their "autonomy bubble" as they demonstrate reliability in specific contexts, rather than attempting full autonomy immediately.

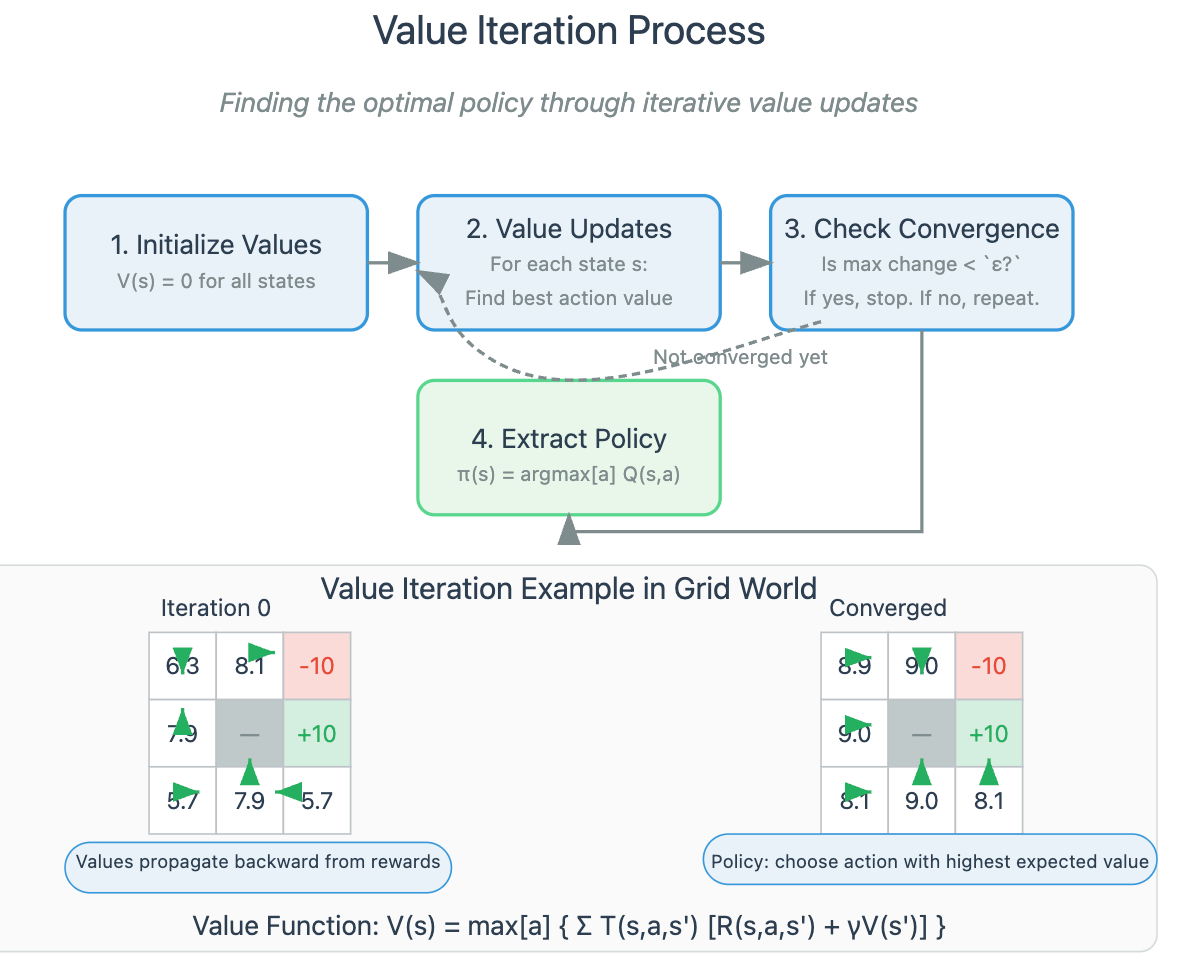
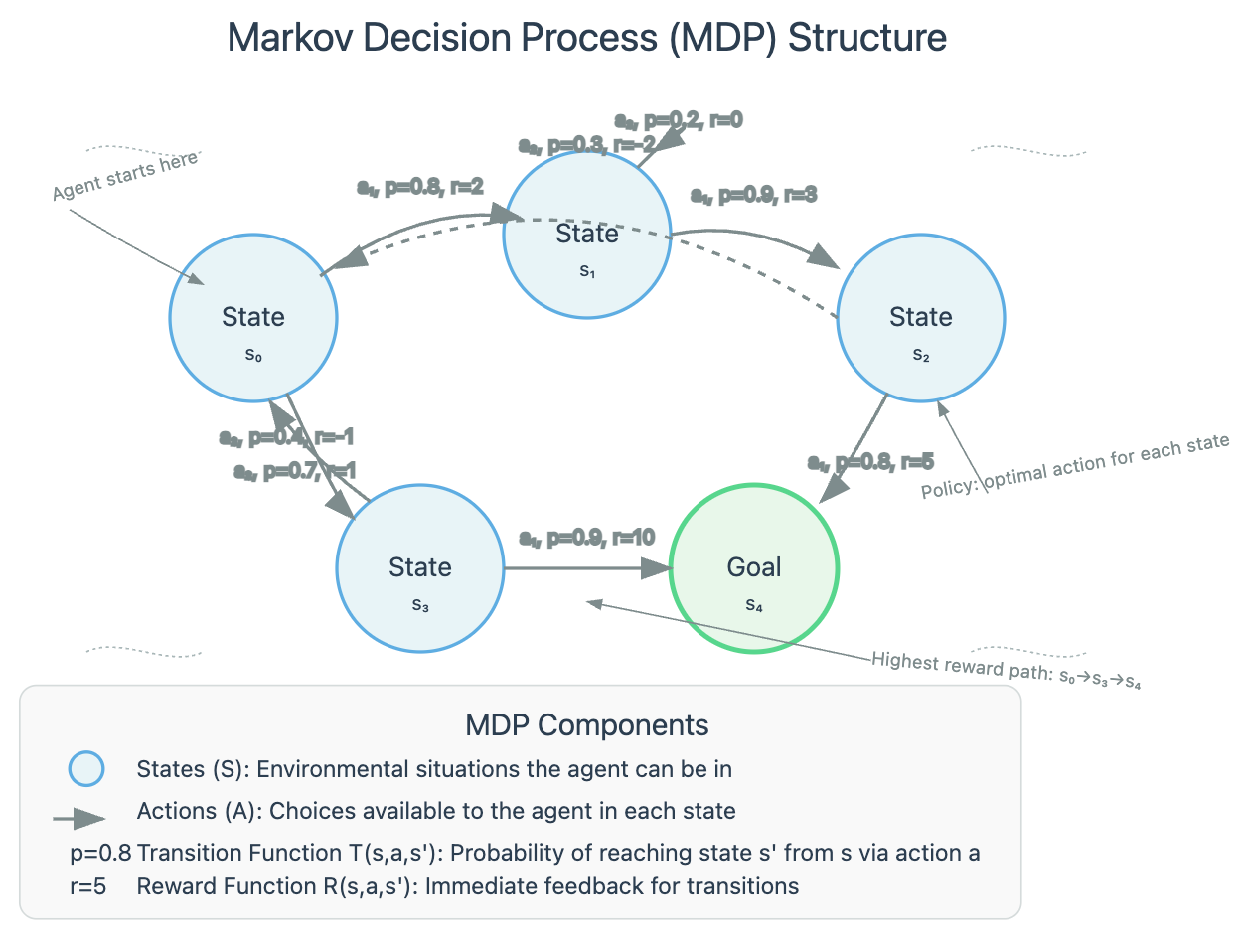
Markov Decision Processes: The Mathematical Foundation

Underlying many agent architectures is the Markov Decision Process (MDP) framework—a mathematical model for decision-making in situations where outcomes are partly random and partly under the agent's control.

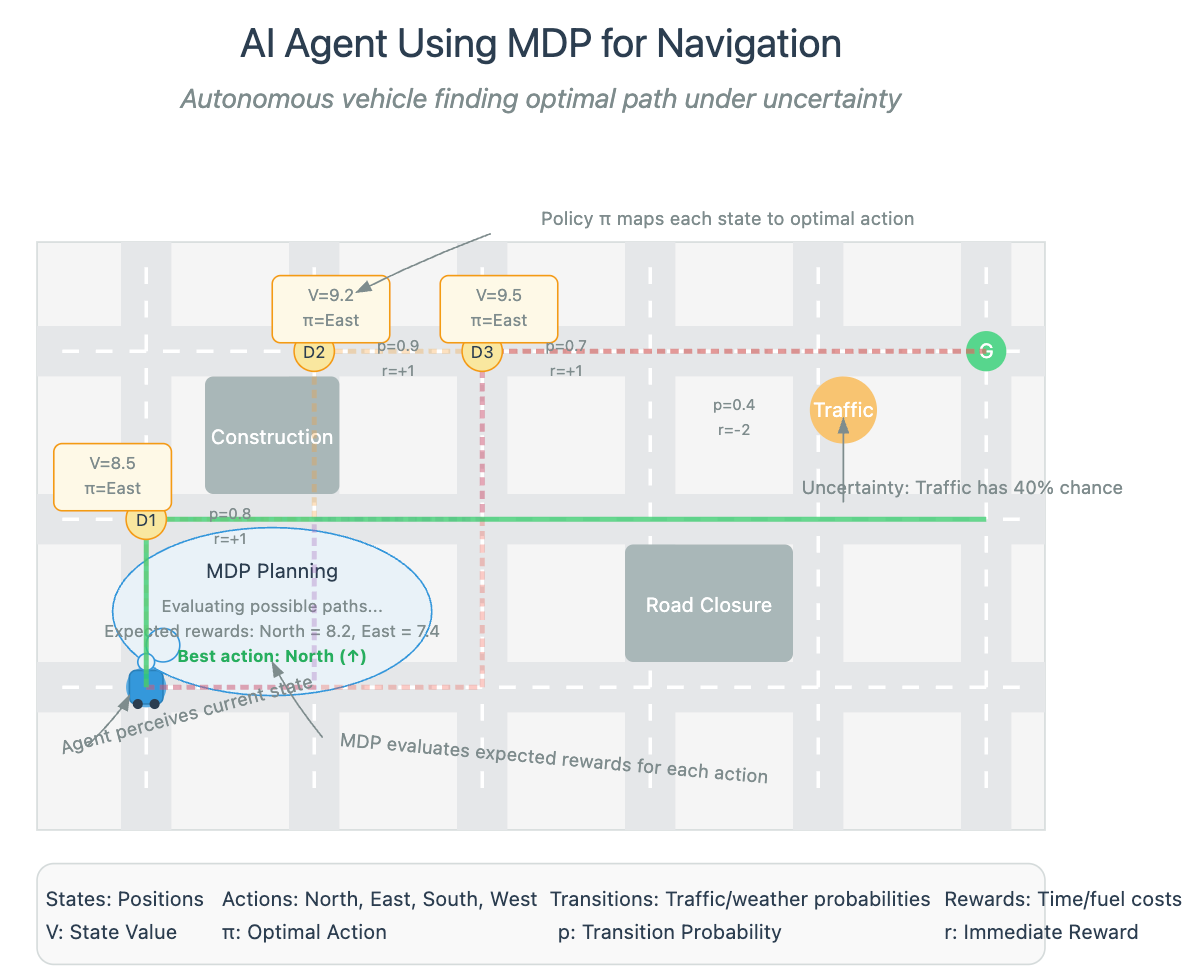
Think of an MDP as a GPS navigation system continually recalculating as you drive. It doesn't just plan a route once; it constantly evaluates the current state, considers possible actions, and selects the one that maximizes expected value.

An MDP consists of:

• States (S): Representations of the agent's situation (e.g., location, battery level)

• Actions (A): Choices available to the agent (e.g., move forward, turn left)

• Transition function (T): Probability of reaching a state given the current state and action

• Reward function (R): Immediate feedback for taking an action in a state

• Discount factor (γ): How much the agent values future versus immediate rewards

What makes MDPs powerful is their ability to balance immediate rewards against long-term payoffs—a crucial capability for realistic agent behavior. Agents solve MDPs to find a policy: a mapping from states to actions that maximizes expected cumulative reward.

Real-World Applications

Autonomous Vehicles

Tesla's self-driving system models driving as an MDP where states include vehicle position, speed, and sensor data about surrounding objects. Actions include acceleration, braking, and steering. The reward function balances safety, efficiency, and passenger comfort.

The non-obvious challenge: Designing reward functions that avoid unintended consequences. Early autonomous vehicle systems rewarded smooth driving but inadvertently encouraged unsafe behavior in edge cases—showcasing the importance of reward shaping.

Recommender Systems

Netflix's recommendation engine uses an MDP approach where states represent user preferences and viewing history. Actions are content recommendations, and rewards come from user engagement.

Implementation insight: These systems must balance exploration (recommending new content types) with exploitation (recommending content similar to what users already enjoy)—a classic tradeoff in reinforcement learning.

Practical Takeaway: Build a Simple MDP Agent

Here's a minimal framework for implementing an MDP-based agent:

class MDPAgent:
    def __init__(self, states, actions, transitions, rewards, discount=0.9):
        self.states = states
        self.actions = actions
        self.transitions = transitions  # P(s'|s,a)
        self.rewards = rewards  # R(s,a,s')
        self.discount = discount
        self.values = {s: 0 for s in states}  # Initialize state values
        self.policy = {s: random.choice(actions) for s in states}  # Random initial policy
    
    def value_iteration(self, iterations=100, threshold=0.01):
        """Compute optimal state values and policy using value iteration"""
        for _ in range(iterations):
            delta = 0
            for s in self.states:
                v = self.values[s]
                # Calculate value for each action, choose best
                action_values = []
                for a in self.actions:
                    value = 0
                    for s_next in self.states:
                        # Expected value: probability × (reward + discounted future value)
                        value += self.transitions[(s, a, s_next)] * \
                                (self.rewards[(s, a, s_next)] + self.discount * self.values[s_next])
                    action_values.append(value)
                
                # Update state value and policy
                self.values[s] = max(action_values)
                self.policy[s] = self.actions[action_values.index(self.values[s])]
                
                delta = max(delta, abs(v - self.values[s]))
            
            if delta < threshold:
                break  # Converged
    
    def act(self, state):
        """Select action according to current policy"""
        return self.policy[state]

Try implementing this with a simple grid world environment, where the agent navigates from a starting position to a goal. This exercise will give you intuition for how agents balance immediate rewards against long-term goals.

The key takeaway: MDPs provide a principled framework for reasoning about sequential decision-making under uncertainty—the core challenge facing any sophisticated AI agent.

Next week, we'll explore how to handle environments where the agent cannot directly observe the full state, introducing Partially Observable MDPs (POMDPs) and belief states. Until then, experiment with your MDP implementation and observe how changes to rewards and transition probabilities affect agent behavior.